Lyapunov稳定性分析

李雅普诺夫稳定性

李雅普诺夫稳定是一种用于判断动态系统平衡点稳定性的理论，它描述了当系统从平衡状态收到微小扰动时，系统的状态如何变化。

稳定性分析

对于一个状态方程，如果系统的平衡点是，那么该点的李雅普诺夫稳定性可以从以下几个方面进行讨论：

1. 李雅普诺夫稳定性（Lyapunov Stability）：

   如果系统从平衡点受到一个微小扰动之后，系统状态始终停留在的某个小邻域内，则称平衡点是李雅普诺夫稳定的。

2. 渐近稳定（Asymptotically Stable）：

   如果平衡点是李雅普诺夫稳定的，并且系统状态随时间趋向于，即，则称平衡点是渐近稳定的。

3. 全局渐进稳定（Globally Asymptotically Stable）：

   如果无论初始状态在哪里，系统的状态最终都会趋于平衡点，则称该平衡点是全局渐进稳定的。

稳定性判断

李雅普诺夫稳定性分析可以通过李雅普诺夫函数（Lyapunov Function）。它是一种类似于能量函数的构造，用来研究系统状态的变化趋势。

李雅普诺夫函数的构造

一个函数被称为李雅普诺夫函数，需要满足以下条件：

1. 正定性（Positive Definite）：

   $$V(x)>0\text{ 对于 }x\neq x_0\text{,且}V(x_0)=0\text{。}$$

   （即：函数在平衡点外为正，平衡点处为零）

2. 函数的负定导数（Negative Definite Derivative）
   计算李雅普诺夫函数沿着系统轨迹的导数：

   $$- \dot{V}(x)=\frac{\partial V}{\partial x} f(x)$$

   如果在处，说明系统的状态会趋向于平衡点。

3. 渐进稳定的条件：
   若对所有的成立，则平衡点是渐进稳定的。

4. 全局渐进稳定的条件：
   如果李雅普诺夫函数在整个状态空间内都是正定的，并且其导数也是负定的，则该点是全局渐进稳定的。

MATLAB代码实现

% 定义系统向量场
[x1, x2] = meshgrid(-2:0.5:2, -2:0.5:2);
% 定义状态方程
dx1 = -x2;
dx2 = x1;

% 绘制相平面
figure;
quiver(x1, x2, dx1, dx2, 'r');
xlabel('x_1'); ylabel('x_2');
title('稳定性分析');
axis equal;

其中的定义状态方程可以换成需要设置的对应的状态方程，下面给出一些典型的用于稳定性分析的状态方程的公式和图像分析：

• 李雅普诺夫稳定但不渐近稳定的系统

  $$\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \end{bmatrix} = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$$

  

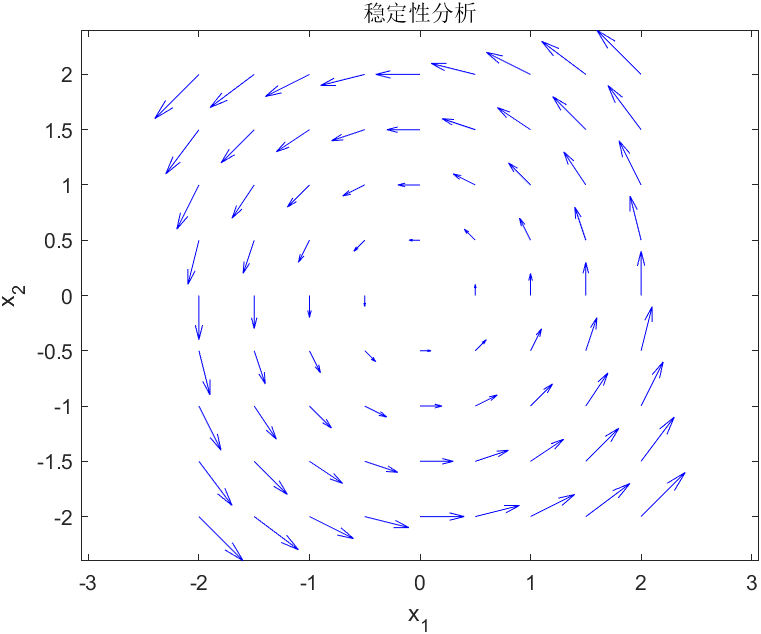
• 渐进稳定系统

  $$\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$$

  

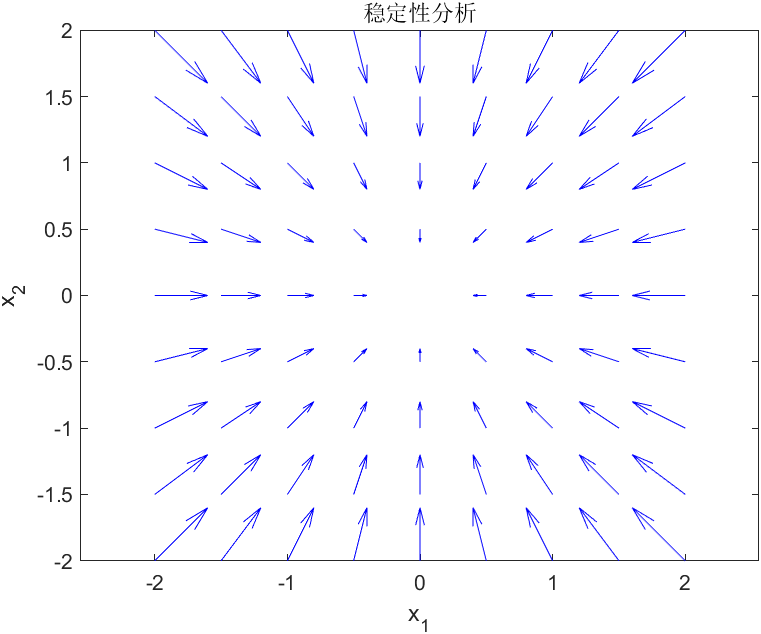
• 非线性全局渐进稳定系统

  $$\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \cdot \begin{bmatrix} {x_1}^3 \\ {x_2}^2 \end{bmatrix}$$

  

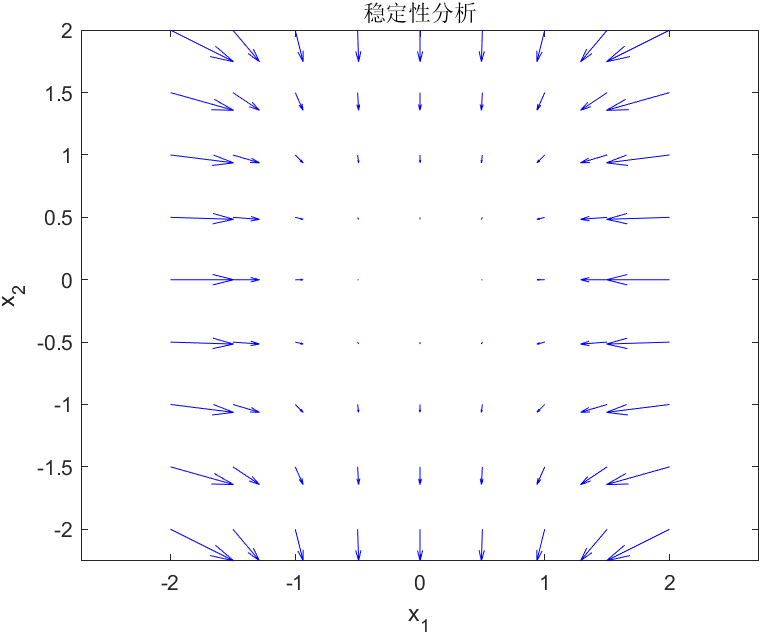
• 不稳定系统

  $$\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$$

  

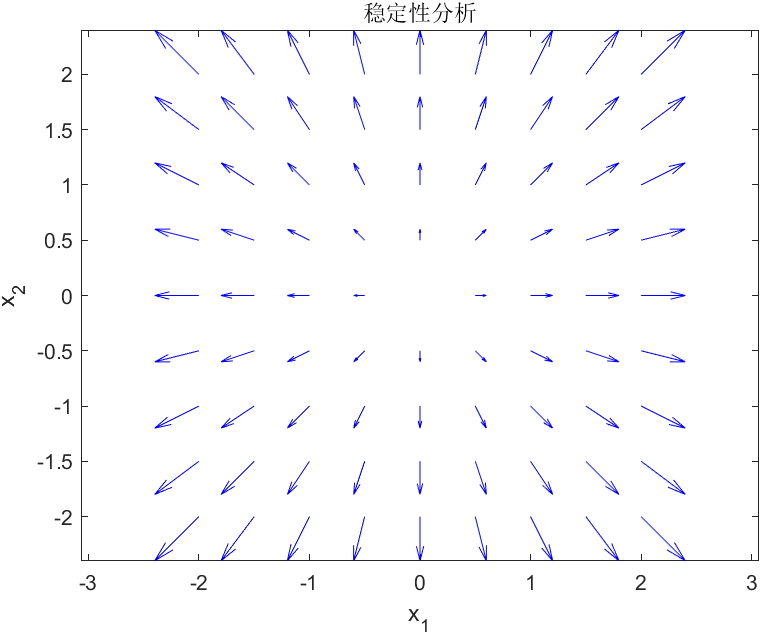
图片绘制工具：MATLAB R2022a